🔐 خوارزمية RSA: كل ما تحتاج معرفته عن أقوى تقنيات التشفير الحديثة
في عالم يتسابق نحو حماية المعلومات وتأمين البيانات، تبرز خوارزمية RSA كأحد أكثر الأساليب الموثوقة لتشفير البيانات وتبادل المفاتيح الآمنة. في هذه المقالة، نأخذك في جولة مفصّلة لفهم RSA، من المفهوم النظري إلى التطبيقات العملية، بأسلوب مهيأ لتحسين الظهور في محركات البحث (SEO).
✅ ما هي خوارزمية RSA؟
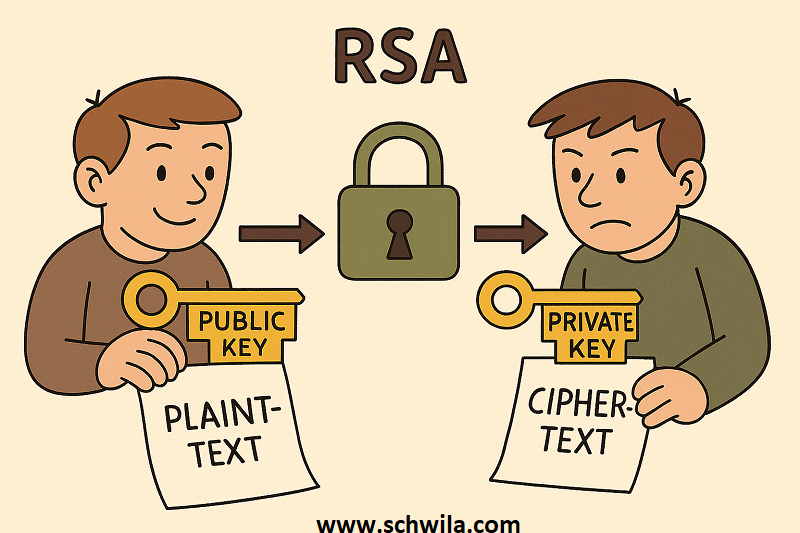
RSA (نسبةً إلى مخترعيها: Rivest–Shamir–Adleman) هي خوارزمية تشفير غير متماثل، تعتمد على مفتاحين:
| مفتاح عام (Public Key) | يستخدم لتشفير البيانات. |
| مفتاح خاص (Private Key) | يُستخدم لفك التشفير. |
تمثل RSA حجر الأساس في أمان الإنترنت اليوم، فهي تُستخدم في:
| توقيع وتوثيق الرسائل الرقمية |
| تبادل المفاتيح الآمنة (Key Exchange) |
| تأمين الاتصالات عبر HTTPS وSSL |
| حماية المحافظ الرقمية والعملات المشفرة |
🔧 كيف تعمل خوارزمية RSA؟
تقوم الخوارزمية على مفاهيم في نظرية الأعداد والضرب الأولي، وتتلخص خطواتها في:
- اختيار عددين أوليين كبيرين: مثل pp وqq، ويحسب n=p×qn = p \times q.
- حساب الدالة ϕ(n)=(p−1)(q−1)\phi(n) = (p – 1)(q – 1)
- اختيار مفتاح التشفير العام ee بحيث:
- 1<e<ϕ(n)1 < e < \phi(n)
- وee لا يُقسم ϕ(n)\phi(n)
- حساب المفتاح الخاص dd:
- بحيث (d×e)mod ϕ(n)=1(d \times e) \mod \phi(n) = 1
- التشفير: الرسالة MM تُحوّل إلى رقم ثم تُشفّر بـ:
C=Memod nC = M^e \mod n
- فك التشفير: باستخدام المفتاح الخاص:
M=Cdmod nM = C^d \mod n
🧪 تطبيق عملي بسيط
لنفترض الأعداد الصغيرة التالية لاختبار الفكرة:
- p=61p = 61, q=53q = 53 ⟶ n=3233n = 3233
- e=17e = 17
- نحسب d=2753d = 2753
إذا أردنا تشفير الرقم 65 (يمثّل نصًا بعد التحويل):
- C=6517mod 3233=2790C = 65^{17} \mod 3233 = 2790
ولفك التشفير:
- M=27902753mod 3233=65M = 2790^{2753} \mod 3233 = 65
💡 بالطبع، في الواقع تُستخدم أعداد بطول 2048 بت لضمان الأمان!
🛠️ أهم تطبيقات RSA في الحياة الواقعية
| شهادات SSL/TLS: لتأمين مواقع الويب |
| بروتوكولات VPN |
| أنظمة البريد الإلكتروني المشفّرة مثل PGP |
| أنظمة الدفع الرقمية ومحافظ العملات المشفّرة |
⚔️ هل يمكن كسر RSA؟
صعوبة RSA تأتي من استحالة تحليل الأعداد إلى عواملها الأولية عندما تكون ضخمة. حتى باستخدام الحوسبة الكمية، لم يُكسر RSA تجاريًا حتى الآن، لكن هناك مخاوف مستقبلية مع تطور الحواسيب الكمية.
📌 أفضل الممارسات عند استخدام RSA
- استخدم مفاتيح بطول لا يقل عن 2048 بت (أو 3072 لمستوى أعلى)
- لا تُشفّر البيانات الطويلة مباشرة باستخدام RSA، بل استخدمها لتبادل مفاتيح (Hybrid Encryption)
- تجنّب استخدام نفس الزوج من المفاتيح في أماكن متعددة
🧠 خلاصة المقالة
RSA ليست مجرد خوارزمية، بل هي ركيزة من ركائز الأمان الرقمي الحديث. سواء كنت مطوّرًا، أو باحثًا في الأمن السيبراني، أو حتى مجرد مستخدم واعٍ، فإن فهم طريقة عمل هذه التقنية يعزّز قدرتك على حماية بياناتك ومستقبلك الرقمي.